Mandelbrot Set
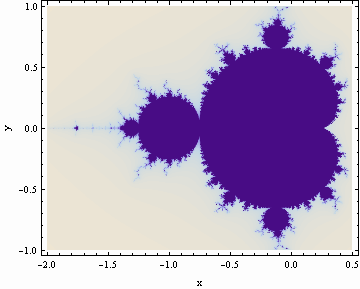
The Mandelbrot set was introduced in 1980, showing how complex phenomena could be generated from simple rules iterated repeatedly. The Mandelbrot set is formed by iterating z = z2 + c for all values of c = x + i y, with an initial value of z = 0. For different complex numbers c, many of the points generated by iterating z2 + c escape to infinity. Those that do not are in the Mandelbrot set.
Benoit Mandelbrot, often referred to as the father of fractals, almost single-handedly created a new geometry of nature. This new mathematics, with a physics base, has fundamentally altered our view of the universe. It is based on the concept of using simple rules to generate complex structures. According to Mandelbrot, fractals themselves "are irregular geometric shapes having identical structure at all scales." In his 1967 paper "How long is the coast of Britain? Statistical self-similarity and fractional dimensionally?" Mandelbrot identified the concept of length as dependent upon the choice of measuring instrument. He introduced the concept of fractal dimension by suggesting that the dimension of a coastline, for example, must fall somewhere between the dimensions of a smooth curve (with dimension one) and a smooth surface (with dimension two).
Based on content from The Mathematical Explorer written by Stan Wagon
