Exploring Escher Patterns

What pattern will a square rubber stamp (a motif) and a design idea (a signature) produce? Using intricate motifs and design ideas, Escher created some of the most stunning mathematical art ever. Try your hand at creating some simple patterns here.

First, choose a motif to use. It is suggested that you initially work with the happy face motif because it will best illustrate how the signature affects the Escher pattern.

Motif Tiles
Happy Face	Pattern 1	Pattern 2	Pattern 3

Now, choose a signature, which is a set of rotations for the selected motif. Escher carved a square tile with his motif and then printed a larger square block with four copies of the motif, each rotated from the original according to a 2 x 2 matrix. Using his notation, 1 indicates no rotation, 2 means a rotation of 90 degrees, 3 means a rotation of 180 degrees, and 4 means a rotation of 270 degrees. Note that all rotations in Escher patterns are counterclockwise.

Signature	Color
{{1, 2}, {2, 1}} {{1, 4}, {2, -1}} {{1, -4}, {-3, 2}}	Teal Brown Tan

For example, using the signature {{1, 2}, {2, 4}} with a 2 x 2 matrix, the original motif will not be rotated in the upper-left corner of the matrix. However, it will be rotated 90 degrees in the upper-right and lower-left corners and 270 degrees in the lower-right corner. This 2 x 2 archetype is then repeated several times vertically and horizontally to yield the complete Escher pattern.

Now click the Visualize button below to produce a block that translates the original tile using the chosen motif and signature.

Many variations are possible in addition to those detailed here.

---

You can take the tile, as Escher did with ink and woodcut, and use it to create a repeated pattern in the plane. You can generate a nice variety of patterns using the rules shown above. How many different patterns can you find? Different signatures can lead to essentially the same pattern. For example,

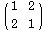
and

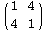
lead to congruent patterns.

Compare the results of these two signatures by entering {{1, 2}, {2, 1}} and {{1, 4}, {4, 1}}, each in turn. These patterns are rotated versions of the same pattern. Escher successfully counted the number of truly different patterns there are when rotations are used as the only variation. How many patterns can you find?

Based on content from The Mathematical Explorer written by Stan Wagon