エッシャーの絵の探究
四角いゴム印(モチーフ)とデザインのアイディア(シグネチャ)でどんなパターンができるでしょうか.複雑なモチーフとデザインのアイディアを使って,エッシャーは数学アートの中でも代表的なもののいくつかを作りました.ご自分でも,簡単なパターンを作ってみませんか.
まず,モチーフを選んでください.「ハッピーフェース」のモチーフがエッシャーのパターンにシグネチャが与える影響を最もよく表すので,最初はこのモチーフを選ばれるといいでしょう.

ここに詳述した以外にも,たくさんのバリエーションが可能です.

エッシャーがインクと木版でしたように,タイルを使って平面に繰返しのパターンを作ってみましょう.上記の規則を使って変化に富んだいろいろなパターンを作ることができます.異なるパターンはいくつあるでしょうか.シグネチャを変えても,基本的には同じパターンが生まれます.例えば,
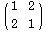
と
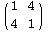
では合同のパターンになります.{{1, 2}, {2, 1}}と{{1, 4}, {4, 1}}を交代で入力して,この2つのシグネチャを使った結果を比べてください.同一パターンを回転したバージョンが生まれます.エッシャーは回転を唯一の変化として採用した際の,本当に異なるパターンだけを数えることができました.貴方が見付けられたパターンはいくつですか.
この内容はStan WagonによるThe Mathematical Explorer に基づいています.

