Random Bicycle Tracks
If you came across a set of bicycle tracks in the mud, could you determine which way the bicycle was going simply by examining the tracks? Sherlock Holmes goofed with this problem. More explanation is below.
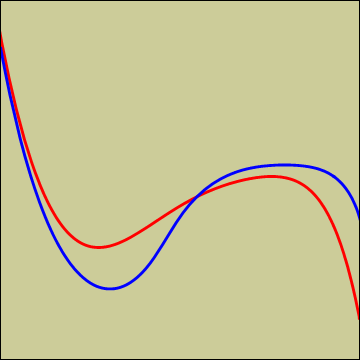
Assuming that these curves represent the tracks a bicycle has left in the mud, can you determine whether the bicycle traveled from left to right or from right to left?
In "The Adventure of the Priory School" Sherlock Holmes was faced with a problem involving bicycle trails left in some mud. His task was to determine the bicycle's direction of travel solely from an examination of the tracks. He had more information than you will have since he could look at the physical tracks and, for example, see which track was deeper.
Although Holmes considered only the weight of the rear wheel in trying to find the direction of the bicycle, he should have thought about this problem in mathematical terms. Here is the explanation Holmes should have given Watson:
The key point, Watson, is to realize that the rear wheel of a bike always points to the place where the front wheel touches the ground. We can clearly identify the rear track by noting that it crosses over the front one. Then we just pick two random points on the rear track and look at the tangents to the curve at those points. By marking the points where the tangents cross the front track and measuring the segments, we can see which direction yields segments of the same length. Since a bicycle cannot change its length, this tells us the direction of travel.
And further, Watson, we can tell the rear track from the front by this tangent method as well, even if we could not discern which track was more deeply sunk or which crossed over the other at the crossing points.The following diagram illustrates the preceding explanations.
Tangents from the blue curve at the bumps completely fail to strike the other curve, so the blue curve cannot be the rear track. Now we look at the two red points on the rear track and look at where their tangents hit the front track (black dots). The only length common to both sets of tangent segments is the one shown as a thick yellow line. This means that the tracks were going from right to left.
Based on content from The Mathematical Explorer written by Stan Wagon
