ランダムな自転車の轍
ぬかるみの中の自転車の轍から,その自転車がどちら向きに走って行ったかお分かりになりますか.シャーロックホームズはこの問題で失態を演じてしまいました.以下で詳細をご覧ください.
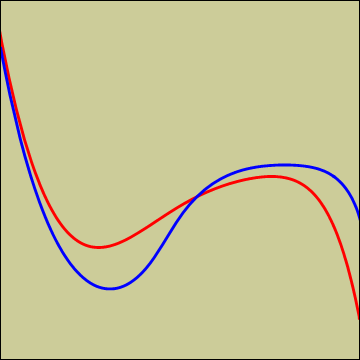
この曲線は自転車がぬかるみに残した轍を表しているとします.この自転車は左から右へ走っていたのでしょうか.それとも右から左へ走っていたのでしょうか.
「プライオリ学校」の中で,シャーロックホームズはぬかるみの中に残された自転車の轍についての問題に遭遇しました.彼はこの轍だけから自転車が走った方向を決定しなければなりませんでした.彼は今ここにある以上の情報を持っていたのは確かです.なぜなら,彼は実際にその轍を見て,例えばどちらの轍のほうが深いかなどを確かめることができたからです.
ホームズは後輪の重さのみを考慮して,自転車の走った方向を判断しようとしました.しかし,彼は数学的見地からこの問題を考えるべきだったのです.以下が,ホームズがワトソンにすべきだった説明です.
ワトソン君,この問題を解く鍵は自転車の後輪は常に前輪の接地点を向いているということなのだよ.後輪の跡は前輪の上を通っているから,轍を見ればどちらが後輪の跡なのかがはっきり分かる.それから後輪の軌跡上にランダムに2点選んで,これらの点での曲線に対する接線を引く.接線が前輪の跡と交わる2点に印を付けて接点からのそれぞれの距離を測ると,どちら向きだとランダムな2点の接線の線分の長さが同じになるかが分かる.すると,自転車の大きさは変わらないのだから,その自転車が走った方向が分かるのだ.
そしてさらに,ワトソン君,たとえどちらの軌跡がより深く沈んでいるか分からなかったり,交点を見てもどちらが先につけられた跡なのか分からなかったとしても,この接線を使った手法を使うと,どちらが前輪の軌跡でどちらが後輪の軌跡なのかも分かるのだ.下の図は,この説明を図解したものです.
青の曲線の接線は隆起点で完全にもう一方の曲線から離れていっているため,この青い曲線は後輪の跡にはなり得ません.後輪の軌跡上の赤い2点について,その接線が前輪の軌跡と交わっている点(黒い点)を見てみます.2本の接線の線分について同じ長さになるものが黄色の太線で示されています.これにより,この軌跡が右から左に描かれたものだということが分かります.
この内容はStan WagonによるThe Mathematical Explorer に基づいています.
