|
|
|
|
|
|
 |
 |
|
Chaotic Pinball Billiards
|
|
|
|
|
|
| Organization: | SUNY at Buffalo |
|
|
|
|
|
|
0210-531
|
|
|
|
|
|
1999-08-20
|
|
|
|
|
|
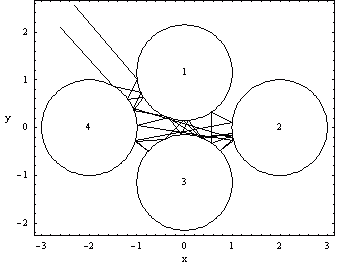 The scope of this software is to help students to learn and understand classical and chaotic scattering through hard or inelastic lattices on one hand but on the other hand the package is powerful enough for researchers to study new two dimensional lattice configurations like Penrose lattices. The package helps studying scattering properties chaotic or statistical, such as the decay rate of particles, the fractal dimensions of the repellers, the system entropies and the deflection functions. These properties can be studied with only a little effort from the user.
The pinballs machine involves a metallic sphere and a stadium. The interesting part of the stadium is the central three-disk (usually) system. When the ball touches one of these disks the disk suddenly reacts in a way that shoots the ball racially outward. After a number of collisions this system ends up like a "particle accelerator".
The important thing to have in mind here is that in classical mechanics time is reversible. That is if you roll a ball down the hill, and then you push it back up the hill, the same equations still apply. This fact permits us to use results taken by studying pinball scattering to describe real inelastic lattice scattering. In real lattices the disk absorbs energy from the particle slowing it down, instead of accelerating it as in the pinballs case.
|
|
|
|
|
|
|
|
|
|
|
|
Chaos, Nonlinear, Dynamics, chaotic, scattering, pinball, disk, fractal, dimension, Hausdorff, Information, Poincare, Lyapunov, entropy, Kolmogorov, Sinai
|
|
|
|
|
|
| PinballBilliards.zip (1.9 MB) - Zip archive |
|
|
|
|
|
|
|
| | | | | |
|
For the newest resources, visit Wolfram Repositories and Archives »
