|
|
|
|
|
|
 |
 |
|
Colored Zonotiles
|
|
|
|
|
|
|
|
|
|
|
|
0211-194
|
|
|
|
|
|
2005-03-03
|
|
|
|
|
|
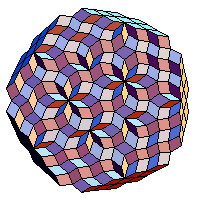  The generalization of Penrose tilings by two rhombs, is a tiling by zonogons (paralled-sided, centrally-symmetrical polygons), in which rhombs, hexagons, octagons, decagons etc. of many shapes arise. These tilings are quasi-periodic, and are related to quasicrystals. Two constructions for such tilings were set forth by DeBruijn in 1981: the generalized dual method, and the generalized projection method. The former is implemented here. The tilings fill a finite region of the plane, itself bounded by a zonogon; I call this region a zonotile. Methods are supplied to sort the polygons of the zonotile according to surface area, and to assign a distinct color to each set of equal area. (updated by Author, 3 March 2005)
[Image created by 2D_Zonotiles.nb]
The extension of the 2D zonotile function to three dimensions has proved very difficult. For several years I grappled with the problem, only to turn away in frustration. Not only do the methods employed here cost much time, when many planes are involved (say, more than twenty), but it fails outright to create many zonotiles.
Nevertheless, some lovely local space-fillings, of zonohedra tiled by smaller zonohedra, can be obtained. It is a curious fact, though far be it from me to prove this assertion, that, given a zonohedron tiled by some suite of smaller zonohedra, the entire space outside the zonohedron can be tiled by this same suite, as well.
These tilings of zonohedra by smaller zonohedra—these 3D zonotiles—are based upon arrangements of planes. Wherever three or more planes intersect at one point, a zonohedron arises. Any convex polyhedron ipso facto yields an arrangement of planes—the planes of its faces. These faces, produced into infinite planes, intersect, perhaps, in points outside the original polyhedron; and these points are the vertices of various stellations of that polyhedron. The exact relationship between 3D zonotiles and stellations of convex polyhedra seems an especially interesting subject for future study.
[Image created by 3D_Zonotiles.nb]
Updated by author 11 February 2005
|
|
|
|
|
|
|
|
|
|
|
|
zonogon, Penrose tiling, quasi-periodic tiling, generalized dual method, zonotile, polygon
|
|
|
 |
|
|
| 2D_Zonotiles.nb (334.4 KB) - Mathematica Notebook | | 3D_Zonotiles.nb (239 KB) - Mathematica Notebook | | dragonalia.JPG (124.7 KB) - JPEG image | | fifty_decagons.gif (443.8 KB) - GIF image | | flowers_and_stairs.gif (220.3 KB) - GIF image | | roof_d'Archangelo_ii.jpg (84.5 KB) - JPEG image |
|
|
|
|
|
|
|
| | | | | |
|
For the newest resources, visit Wolfram Repositories and Archives »
