|
|
|
|
|
|
 |
 |
|
A Single Construction Method of Steiner Triple Systems
|
|
|
|
|
|
| Organization: | Columbus State University |
|
|
|
|
|
|
2007 Wolfram Technology Conference
|
|
|
|
|
|
Champaign, IL
|
|
|
|
|
|
Abstract
Depending on the number of elements in a set, we may use a different method for constructing a Steiner triple system. For number of vertices v >= 7, if v = 3 (mod 6) we use the Bose construction; if v = 1 (mod 6) we use the Skolem construction. We present a different method which works for either case of v.
The method is based on a different coloring of the vertices from the traditional coloring. A matrix with particular characteristics is created that in turn is used to create a tree. If this tree is traversed from the root to a leaf, a Steiner triple system of a given order is generated. A matrix for v = 7 is shown below.
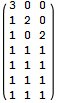
These matrices all have certain characteristics. They have up to v rows. Every row adds up (v-1)/2. The upper-right is filled with 0's. The diagonal to the left of this all-zero section adds up to the number of triples in the system. All the entries below this diagonal are either 0's or 1's. The number of columns is the number of colors needed to color the set. The following is another example for v = 7.
The following are examples of these matrices for v = {9, 13, 15, and 19).
Each tree that is created generates many Steiner triple systems, one for each traversal from the root to a leaf.
|
|
|
|
|
|
|
|
|
|
|
|
http://www.wolfram.com/news/events/techconf2007/
|
|
|
|
|
|
| SteinerTripleSystems.zip (93.5 KB) - ZIP archive [for Mathematica 6.0] |
|
|
|
|
|
|
|
| | | | | |
|
For the newest resources, visit Wolfram Repositories and Archives »
